MULTI-OBJECTIVE DESIGN OPTIMIZATION OF SANDWICH BEAM UNDER 3-POINT BENDING TEST

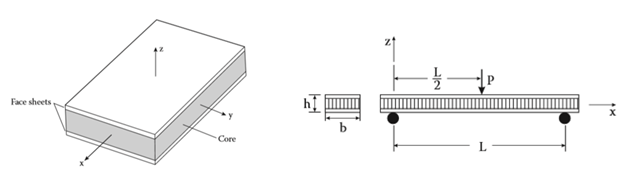
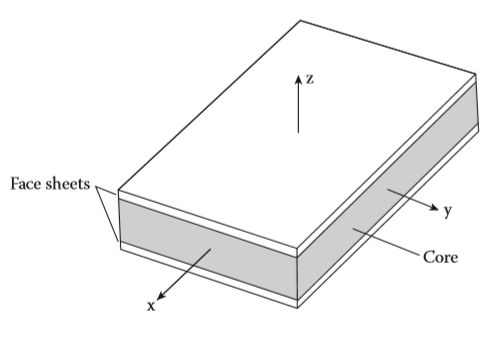
Abstract: As part of the Characterization of Advanced Composites class, conducted by Dr. R. Byron Pipes, we class conducted an experiment to perform a three-point bending test on a sandwich sample. The sandwich samples, as shown in the following figure, were made of Aluminum 6061 on the outside and H80 PVC honeycomb on the inside (as specified in the book Experimental Characterization of Advanced Composite Materials).
The two ends were fixed, and a constant force of P = 80,000 N was applied at the center using the Load Frame machine in the lab. The goal of this experiment was to characterize the sample for its strength by recording the deflection for different geometrical samples.
Several large-scale parts, such as wings in the aerospace industry, use this sandwich combination due to its strong material properties. Without a doubt, this is an expensive set up, given the price of the materials and their sizes. I was interested in knowing whether it was possible to optimize the shape (thickness, length and width) of the samples such that their strength was maximized (least deflection), while at the same time keeping an efficient approach towards the total material used, hence saving on the cost.
The objective of this project was to determine the design parameters a sandwich beam (with Aluminum as face and H80 PVC Honeycomb as core) such as to minimize deflection under 3-point bending test with fixed load, whilst minimizing the weight of the beam.

Brief Summary

• Developed mathematical objective functions and constraints based on test requirements and part GD&T
• Recorded design variables for optimization
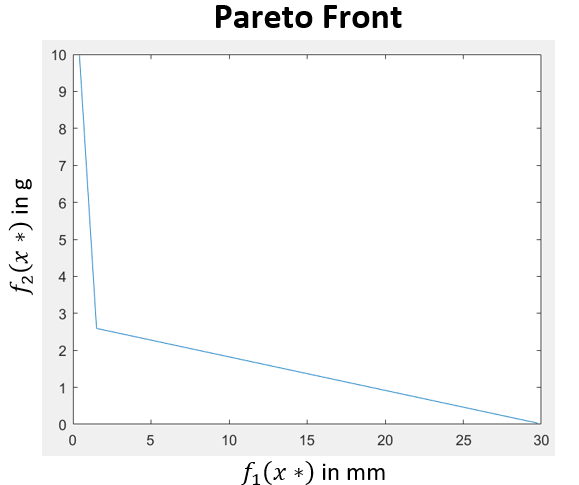
• Performed design optimization via SQP method and obtained Pareto front using MATLAB
• Documented results and performed convergence analysis

Conclusion: Our solution, derived from the SQP algorithm, satisfies all the requirements and constraints. The geometric values derived from the solution abide by the ASTM standards. The computation is not very expensive, since our problem formulas are not too complex. It is observed, however, that it becomes increasingly expensive when we shift our weight towards mass instead of deflection. Since the Langrange multiplier lamda values, along with the constraints are satisfied, SQP satisfies the KKT conditions. Given that out Pareto front does not provide a convex optimum, we can derive the optimal design point depending on our tradeoffs.
This method can be applied on much larger scales. As the example mentioned earlier, several large parts in the industry, such as the wings, have to go through this test. Of course, we want our parts to be extremely durable and structurally sound. However, problems arise when the material to be used is expensive (carbon fiber, etc.). Hence, a trade off must be done to satisfy this problem. Our objective can be easily expanded to larger scales and materials by changing the given properties.